今回は圧縮についてお届けしたいと思います。
圧縮応力ってなかなか、みなさん評価する必要性を感じていないんじゃないでしょうか。
曲げや引張と違って、圧縮は押しつぶされるだけなので大きく変形して壊れるイメージがないからでしょうか。
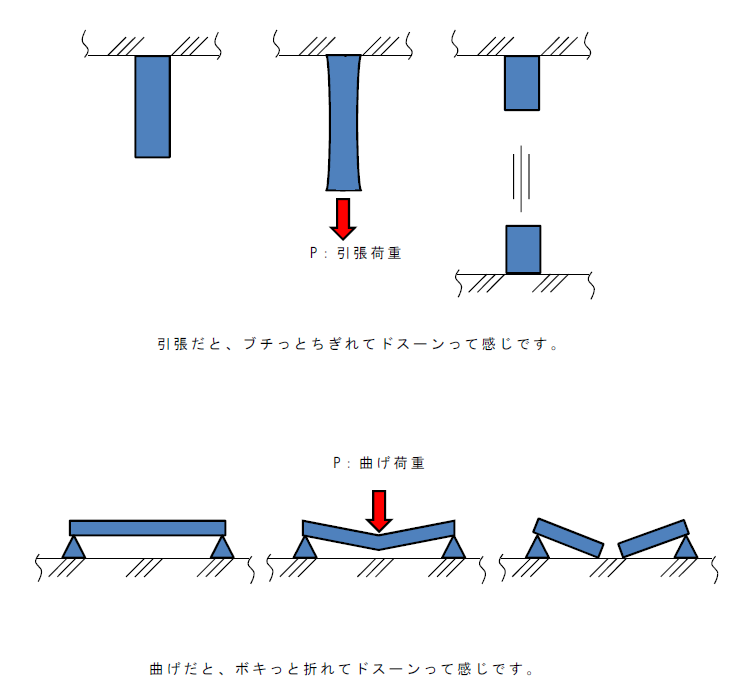
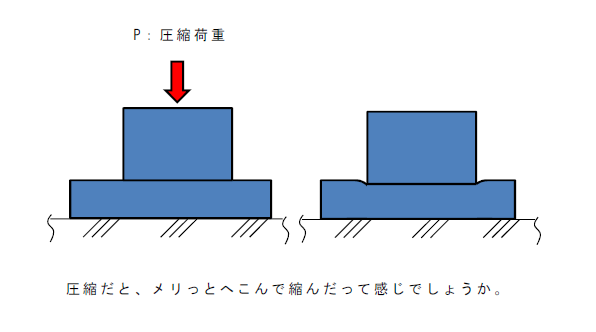
プレートやブロックの形であれば、圧痕がつく程度で大きな事故にはつながらないでしょう。
しかし、柱や梁などの構造部材で特に細長い部材に圧縮が作用して、限界を超えて壊れたとすると大きな事故につながる可能性が出てきます。
この細長い部材に圧縮が作用して折れ曲がってしまうことを座屈といいます。
つまり、単なる圧縮と区別していて、座屈は注意する必要があるということがなんとなく伝わると思います。
というわけで、今回は圧縮の中でも特に細長い部材に作用する場合の座屈について、超簡単にご説明したいと思います。
この記事を読んでいただければ、みなさんはもう座屈マスターです。
それではどうぞ。
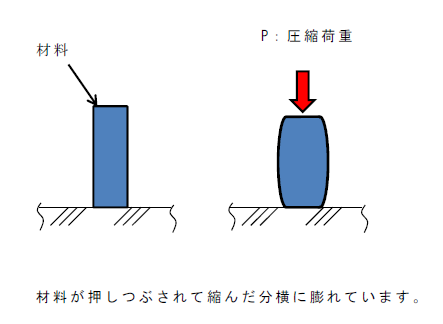
圧縮荷重:P
材料を押し潰そうとしている荷重のことです。
引っ張りとは反対の方向に作用している力のことです。
座屈とは
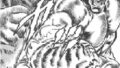
座屈のイメージは、長い棒を短くしようとする方向に力が働いたとき、長い棒が横にポキッと折れてしまうというものです。
硬い鋼材がポキッといくなんてイメージしづらいですが、
わかりやすい画像がないか探してみました。
これです。

座屈しない許容圧縮応力
圧縮の許容応力は、基本的に引張応力や曲げ応力の許容応力と同じです。
つまり、SS400の長期許容応力の場合であれば、\(156N/mm^2\)です。
圧縮の場合は、引っ張りと同じ強さがあります。
ただし、長くない部材の場合です。
長くない部材とは、プレートやブロックのような形状のものです。
では、長い部材の場合の許容圧縮応力がいくつになるのか。
ここからが今回の記事の本題です。
細長比
まず、圧縮部材の細長比:\(λ\)(ラムダと読みます)を求めます。
\(λ=lk/i\)
\(lk\):座屈長さ\((cm)\)
\(i\):断面2次半径\((cm)\)
圧縮材の細長比は、250以下。
柱材の細長比は、200以下。
これらが鋼構造設計規準で示されています。
断面2次半径は、\(i=√(I/A)\)で簡単に求めることができます。
ここに設計技術者の技量の差は出ません。
しかし、次の\(lk\)の長さをいくつに設定できるかが、設計の技量差が現れるところです。
なぜか。
まず専門書などには、lkは以降のように示されています。
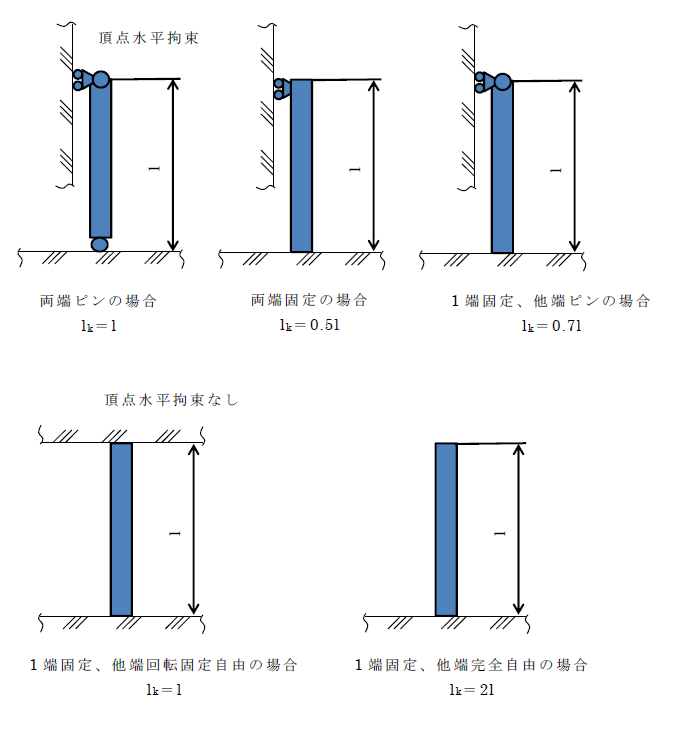
この\(lk\)を適切に選択して、その選択に基づいた設計を実施できるかどうかが問題になります。
つまり、固定端は回転しない接合であり、ピンは回転自由な接合です。
回転自由な端を忠実に設計に反映すると、1例として下写真のようになります。

限界細長比
次に、限界細長比:\(Λ\)(ラムダと読みます。\(λ\)の大文字です)を求めます。
\(Λ=√{π^2E/(0.6F)}\)
\(E\):ヤング係数
\(F\):基準強度→降伏点又は耐力になります。
材料がSS400で厚さ40㎜以下であれば、
\(F=235N/mm^2=235MPa\)
\(E=2.05×10^5 MPa\)
よって、\(Λ\)は
\(Λ=√{π^2×2.05×10^5/(0.6×235)}\)
\(≒120\)
材料がSUS304の場合は、
\(F=205N/mm^2\)
\(E=1.99×10^5 MPa\)
よって、\(Λ\)は
\(Λ=√{π^2×1.99×10^5/(0.6×205)}\)
\(≒126\)
となります。
限界細長比は、式を見てもらえばわかる通り、材質で決まります。
しかし、細長比は長さや固定条件で決まる値です。
よって、細長比が限界細長比を超えるか超えないかで変わってくることが予想できると思います。
細長比が限界細長比以下の場合の許容圧縮応力
細長比が限界細長比以下の場合。\(λ≦Λ\)の場合。
許容圧縮応力:\(fc\)は
\(fc={1-0.4(λ/Λ)^2}F/ν\)
\(ν=3/2+2/3×(λ/Λ)^2\)
細長比が限界細長比を超える場合の許容圧縮応力
細長比が限界細長比を超える場合。λ>Λの場合。
\(fc=0.227F/(λ/Λ)^2\)
というわけで、座屈の許容圧縮応力とは、式を知っていれば簡単に出せるということがご理解いただけたと思います。
まとめ
圧縮応力には細長い部材の場合、座屈という現象があることをお伝えしました。
そして、その座屈をおこさないようにするには、部材に作用する応力が許容圧縮応力以下にする必要があります。
許容圧縮応力は、材質、断面性能、及び座屈長さ:\(lk\)によって決まる値です。
ちなみに、細くなくても座屈はおこります。
細いって言ったのは、イメージしやすいからです。
太い部材でも、細長比をもとに算出した許容圧縮応力を超える応力が作用した場合、その部材は座屈します。
そして、設計技量が問われるのは、座屈長さ\(lk\)のモデル選定とそのモデルに基づいた構造を実際の設計に反映できるかということです。
いかがだったでしょうか。
固定端の条件によって座屈長さ\(lk\)の値がことなることをご紹介しました。
このように固定条件が応力値に影響するのは座屈だけではありません。
曲げモーメント計算にも共通しています。
このあたりは、機会があればまた別の記事でご紹介したいと思います。
最後までお読みくださり、ありがとうございました。