強度計算のせん断について、超簡単にご紹介します。
この記事では、設計検討をちゃちゃっと進めるために、せん断についてさくっと計算する考え方や方法をご説明したいと思います。
強度計算についてお届けするのは今回で3回目になります。
せん断という言葉だとわかりにくいですがラオウの拳だとどうでしょうか。
トラの首が持っていかれちゃってるあれです。
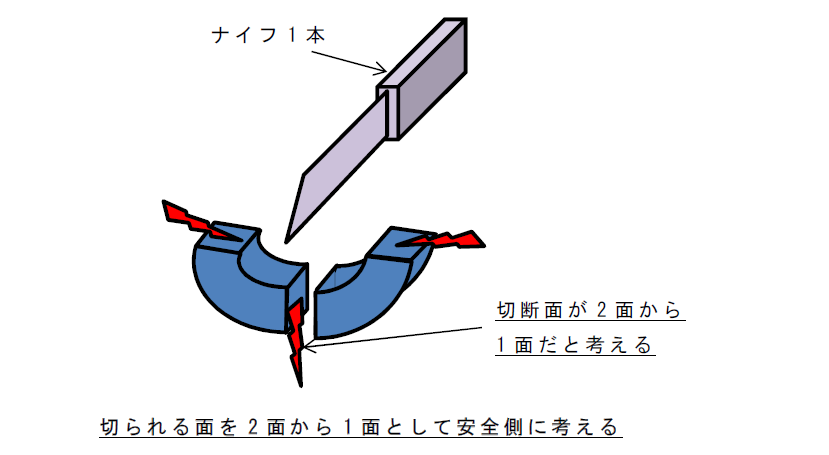
でも私にはラオウのイラストが描けないので、今回はナイフで切るイメージだとしてご説明させてください。
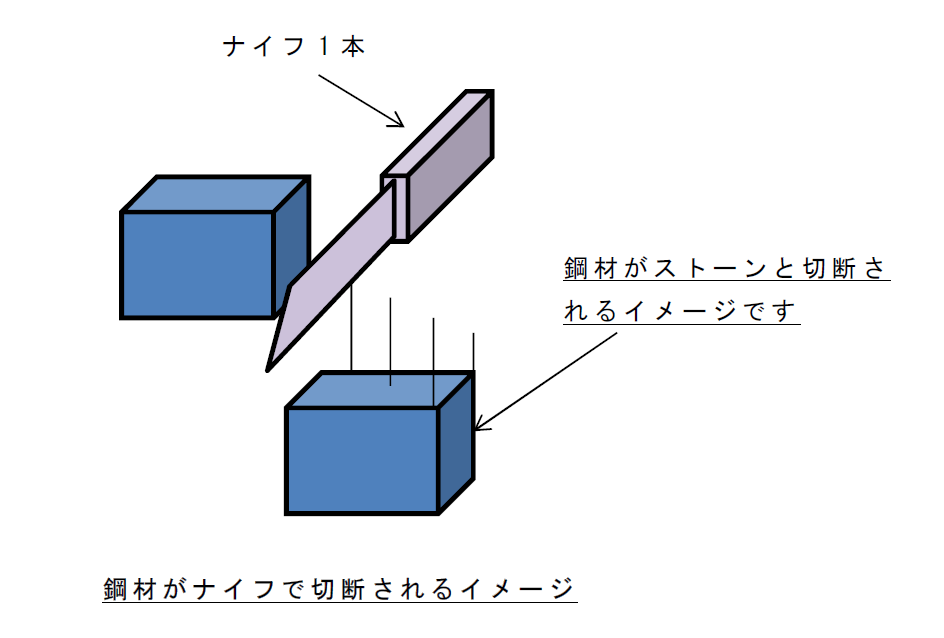
なんとなくイメージできそうでしょうか。
実際に鋼材を切断するのはかなり大きな荷重が必要です。
工作機械のシャーリングなどは、まさに鉄板をナイフで切断するイメージに近いものがあります。
こちらのサイトでわかりやすく写真付きで説明されていますので、ご参照ください。
というわけで、計算式はとても簡単なのでさらっと紹介して、
よく使いそうな設計事例をもとに、せん断荷重による破壊のメカニズムをイラストでご説明してみます。
そして、みなさんのせん断応力の計算技術の向上に少しでもお役に立てればと思います。
それではどうぞ。
せん断応力の計算式
\(τ=P/A\)
\(τ\):せん断応力\((N/mm^2)\)
\(P\):荷重\((N)\)
\(A\):断面積\((mm^2)\)
せん断力が作用している部分の荷重と断面積がわかれば、
簡単に計算できることがこの式でおわかりいただけると思います。
では次にイラストでせん断荷重による破壊のメカニズムを見ていきましょう。
吊り部品
シャックルとプレートなどの構造例です。
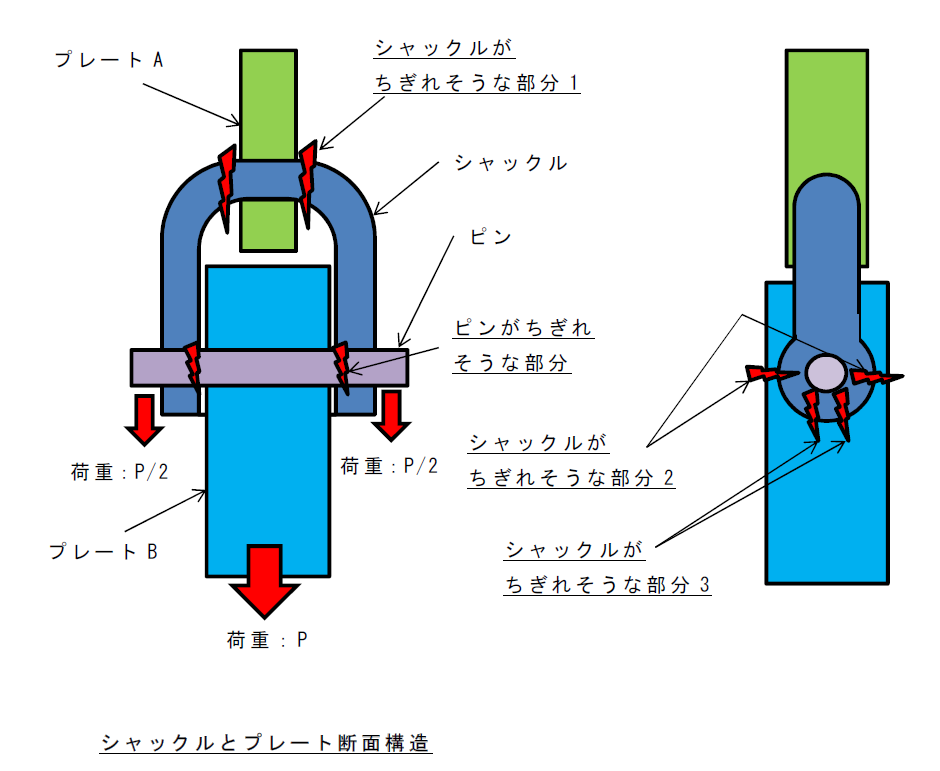
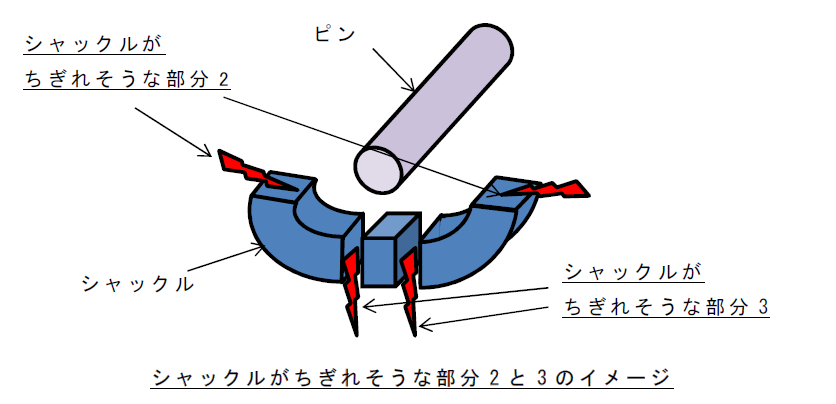
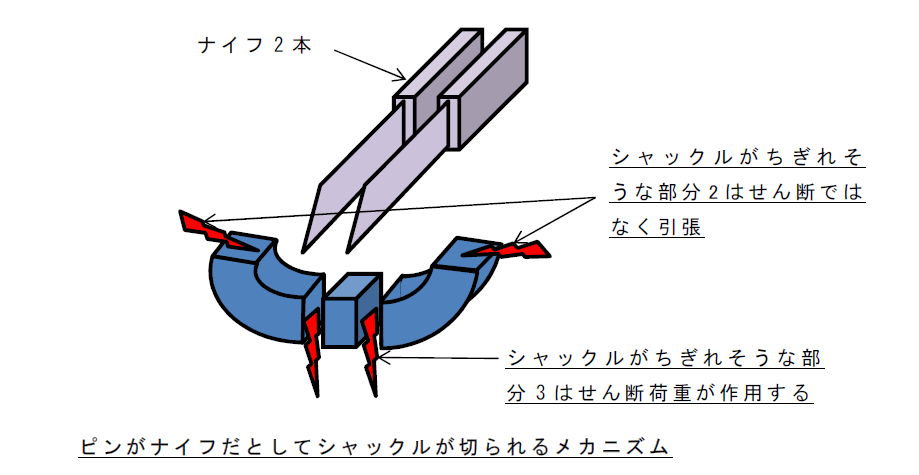
この場合のせん断応力:\(τ\)は、
荷重がピン両端の2カ所に分散されるため、\(P/2\)
断面積がシャックルの断面積で\(A\) とすると
\(τ=P/(2A) (N/mm^2)\)
となります。
固定部品
モータとベースプレート、梁とベースプレートなどの構造例です。
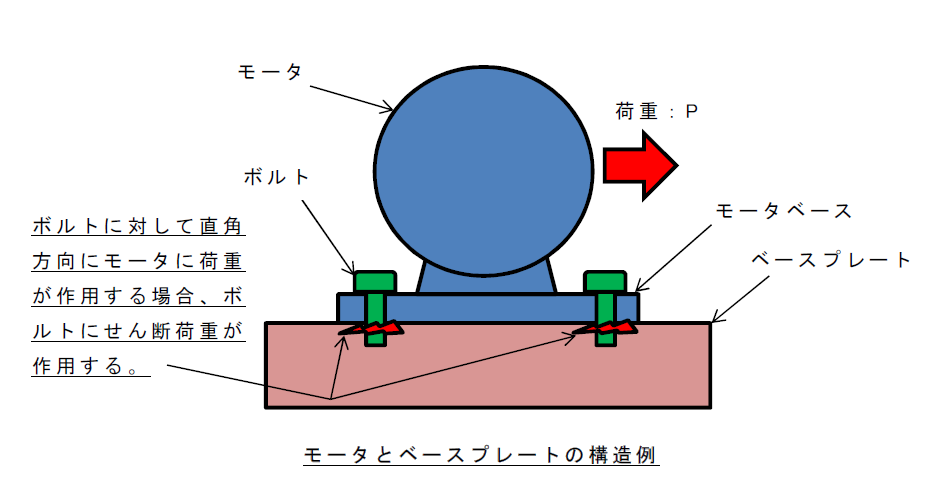
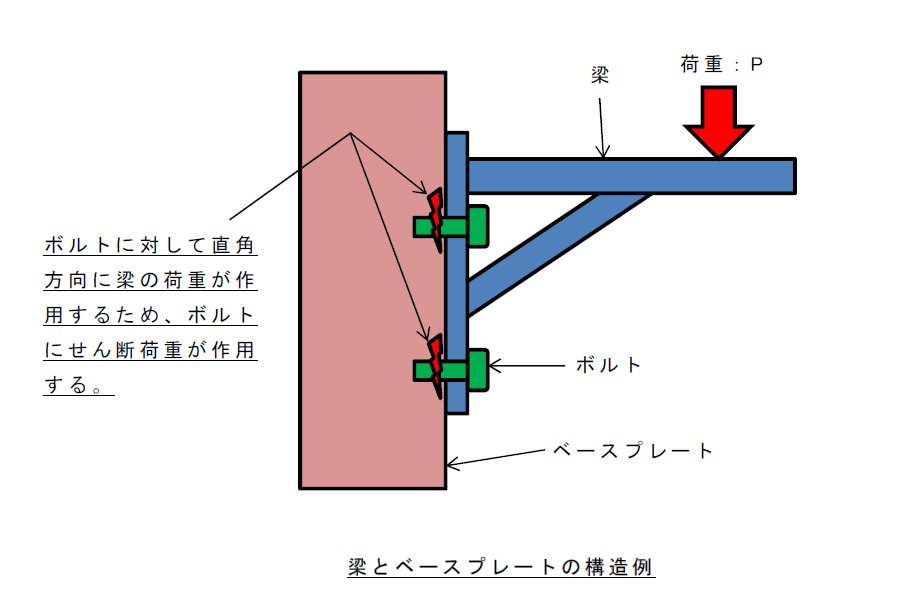
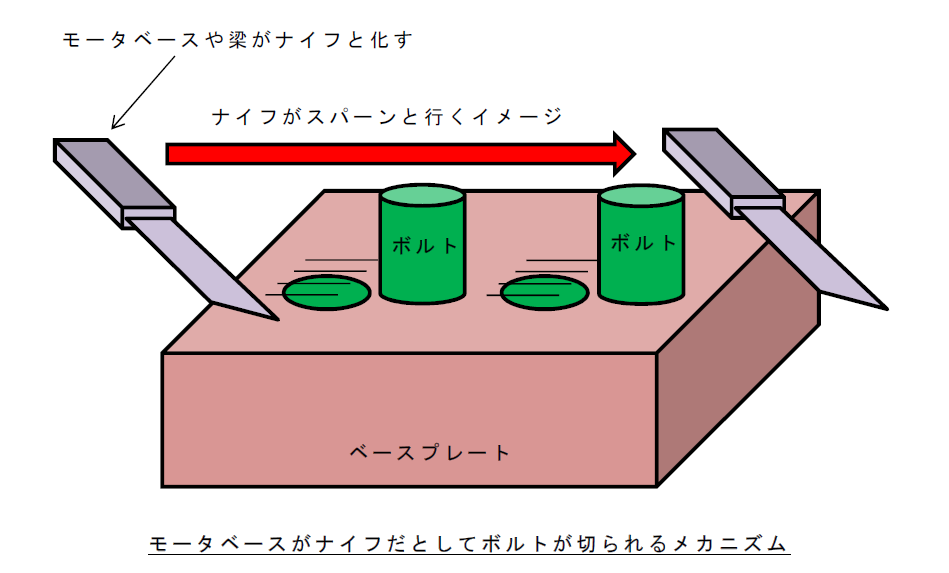
この場合のせん断応力:\(τ\)は、
荷重が\(P\)
断面積はボルトの断面積:\(A\)で2本あるため\(2A\) とすると
\(τ=P/(2A) (N/mm^2)\)
となります。
ボルトの本数が3本や4本の場合は、
分母を\(3A\)や\(4A\)と変更するだけです。
簡単です。
支点部品
梁とピン支点などの構造例です。
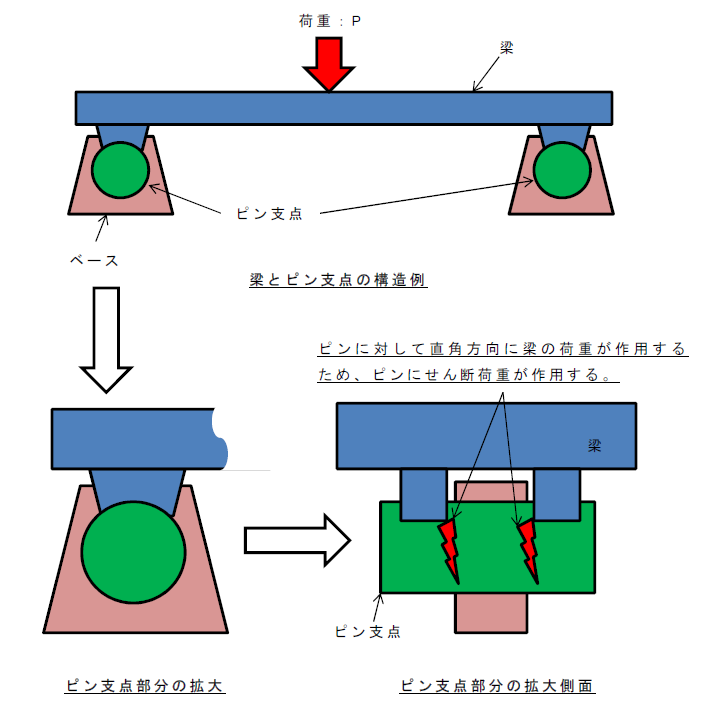
ピン支点部分を梁がナイフと化して切断しているメカニズムがイメージできると思いまいます。
この場合のせん断応力:\(τ\)は、
荷重が梁両端の2カ所に分散されるため、\(P/2\)
断面積がピンの断面積:\(A\)を2カ所切断しているので\(2A\) とすると
\(τ=P/2×1/(2A)\)
\( =P/(4A) (N/mm^2)\)
となります。
まとめ
強度計算のせん断について簡単にご紹介しました。
設計事例として、
・吊り部品のシャックルとプレートの構造
・固定部品のモータとベースプレート他の構造
・支点部品の梁とピン支点の構造
それぞれで切断のメカニズムをイラストでご説明しました。
せん断応力が計算できれば、許容応力と比較して妥当な強度があるかどうかを確認しましょう。
許容応力については、こちらを参照ください。
ただし、せん断応力の許容は、引張や曲げの許容応力を\(√3\)で割った値になるので注意が必要です。
この記事の考え方を身に着けて、みなさんには強度計算を簡単にこなして、設計をバシバシ進められるようになっていただければと思います。
最後までお読みくださり、ありがとうございました。



