動力計算をする時に、みなさん加速力を
きちんと考慮されていますでしょうか。
加速力?
正しい表現としては、加速トルクが適切になると思います。
ちょっとややこしい式を使うので、苦手にされている
方が多いと思います。
今回はこのちょっとややこしい加速力について、ご紹介したいと思います。
この記事を読んでいただければ、また計算機能を使っていただければ
加速力、加速トルクのことを理解できて、簡単に計算できるようになります。
それではどうぞ。
加速時の動力計算式
前回の動力計算の基礎から発展させて、
加速時の動力:Paについてご紹介します。
加速時の動力計算の基本式は、前回と同様で
Pa=m・a・v/(1000) (kW)
です。
前回の一定速度の時の動力計算のときは、
P=m・g・v/(1000) (kW)
でした。
前回では、質量:m の次に重力加速度:gでしたが、
今回は、a:加速度を使います。
単位は同じm/sec^2です。
Pa=m・a・v/(1000)
に対してまず、加速トルク:Ta(N・m)を用いた式に変形します。
Ta=m・a・rから
m・a=Ta/rを
Pa=m・a・v/(1000)の式に代入すると、
Pa=Ta/r・v/(1000)
となります。
また、速度:v=2・π・r・N/60をさらに代入すると
Pa=Ta/r・2・π・r・N/60/(1000)
=Ta・2・π・N/(60・1000)
Pa=Ta・π・N/(30・1000) (kW)
となります。
要するに、加速トルク:Taを計算すれば、加速時の動力は
計算できるということです。
ここで、加速トルクは
Ta=J・α
と表すことができます。
直線運動の式、
F=m・a
と同じような感じです。
Jは慣性モーメントと呼ばれ、質量:mに相当していて、単位は(N・m^2)です。
α は角加速度と呼ばれ、加速度:aに相当していて、単位は(rad/sec^2)です。
α は、角速度:ω (rad/sec)を加速時間:t (sec)で割ったものになります。
α=ω/t
です。
ω は、加速によって増加した分の角速度になります。
t は、加速している時間になります。
よって、加速トルク:Taは
Ta=J・ω/t
となります。
角速度:ω (rad/sec)を回転数:N (rpm) で表すと、
ω=2・π・N/60
となり、これを Ta=J・ω/t の式に代入すると、
Ta=J・π・N/(30・t) (N・m)
となります。
ここで、Nは加速によって増加した分の回転数になります。

残るはJを計算できれば加速トルクが計算できて、
加速動力が計算できることになります。
ここでいったん、加速動力の式を整理しておきます。
Pa=Ta・N・π/(30・1000)
に対して、
Ta=J・N・π/(30・t)
を代入すると、
加速動力:Paは
Pa=J・(N・π/30)^2/(1000・t) (kW)
となります。
J:モータ軸換算の合計した慣性モーメント (kg・m^2)
N:回転数 (rpm)
t:加速時間 (sec)
というわけで、次にJ:慣性モーメントについてご説明します。
慣性モーメント
端的にいうと、物体が回転する時の変化のしにくさです。
つまり、慣性モーメントが大きいと、
回転させようとする力や回転を止めようとする
力も大きな力が必要になるということです。
また、回転力の質量に相当するとも言えます。
言葉で説明するのは難しいので、式と図で説明します。
回転運動させる力はトルクなので、
トルク:Tを慣性モーメント:Jと角加速度:αで表すと
T=J・α
です。
下図を参照ください。

直線運動させる力の式は
F=m・a
です。
下図を参照ください。
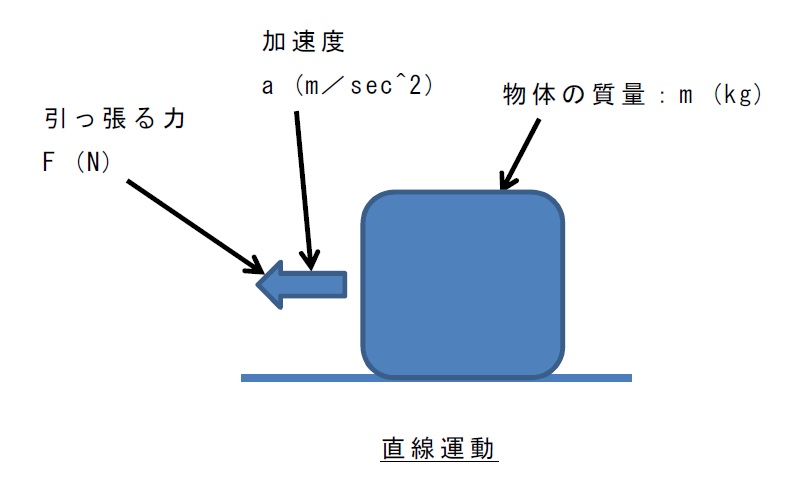
なので、両者の式を比較すると
T=J・α
F=m・a
mに対してJが相当しているように見えます。
つまり、質量です。
しかし、単位は全く違います。
慣性モーメント:J の単位は、kg・m^2
です。
慣性モーメントは、物体の形状や回転半径によって式が異なります。
いろんなサイトで紹介されていますので、一例としてこちらを参照ください。
代表的な形状の慣性モーメントの計算機能を以下に示します。
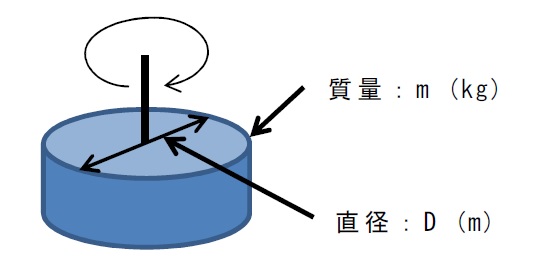
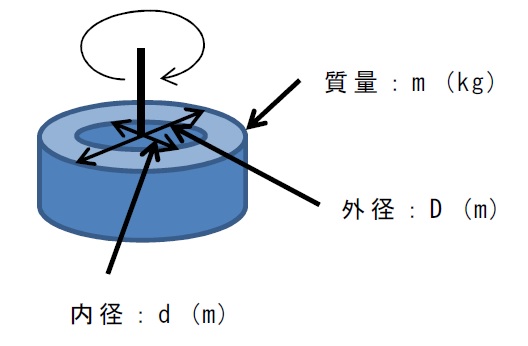

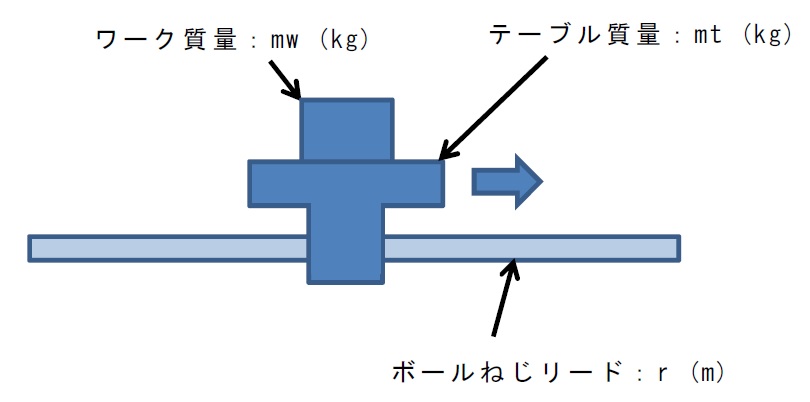
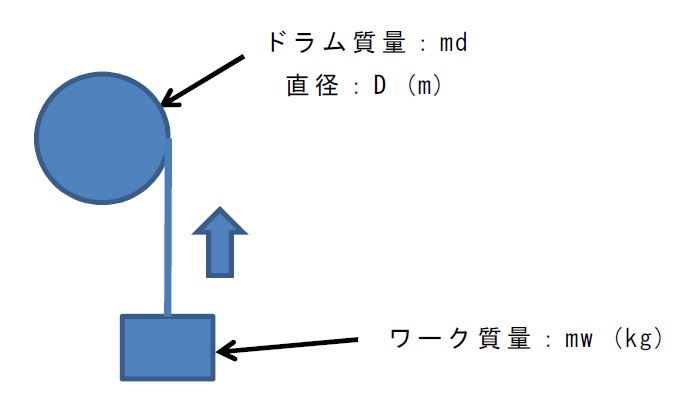
モータ軸換算の慣性モーメント
モータの容量を算出するので、モータにどれだけのトルクが
必要なのかを求めます。
そこで、減速機やギヤ等で回転数を変化させていると
負荷トルクがそれぞれで変化するため、モータ軸基準の
トルクに換算する必要があります。
どうすればよいのかと言うと、それぞれの慣性モーメントに
減速比の2乗をかけるだけでよいです。
簡単です。
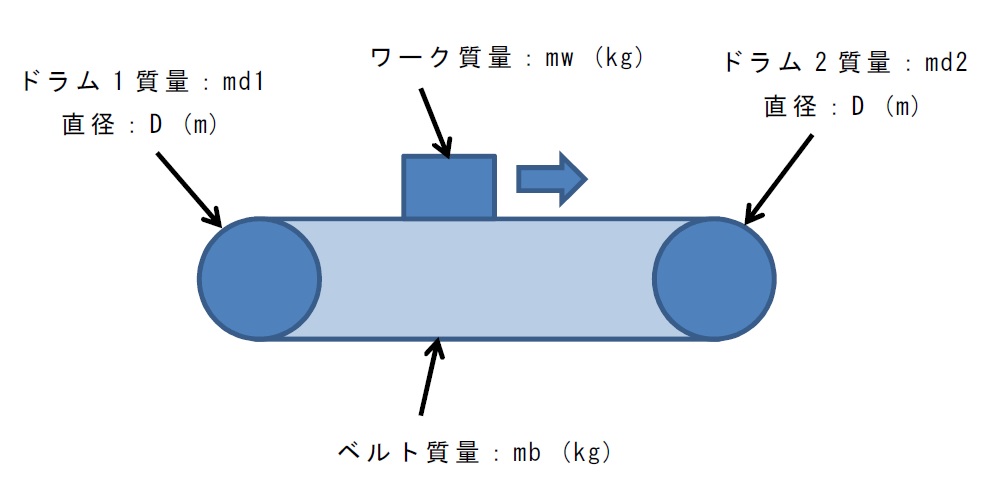
1例として下図を参照ください。
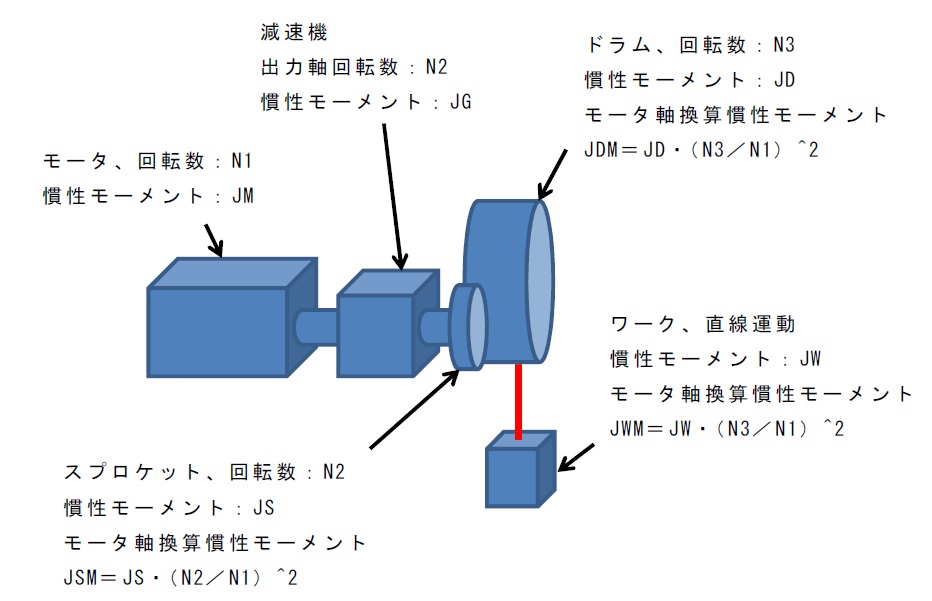
モータ軸換算する時の減速比は、
モータ回転数を分母にして、
該当部分の回転数を分子にした値です。
上図に示す通りです。
上図のモータ軸換算の合計慣性モーメント:Jは
J=JM+JG+JSM+JDM+JWM
となります。
まとめ
前回の動力計算の基礎では、一定速度で
運転している時の動力について計算しました。
そして、今回は加速している時の動力について計算しました。
これらの動力を合計した値を基にモータ容量を決定します。
よって、加速時の動力について計算することを軽んじていると
大きな失敗をする恐れがあります。
加速時の動力が大きく影響しない条件は、
動くものの質量が軽かったり、
ゆっくり加速する場合です。
そうすると大きな動力にはなりませんので、
その見込みがあって計算しない場合が多いと思います。
しかし、いざ運転してみて、動力不足のために
モータ電流の定格値をオーバーするようなことが発覚
した時には、大きな設計見直しとなります。
その結果、大きなコスト損失、工程遅延になります。
そんなことにならないために、この記事を機会に
加速時の動力も計算するようにしてみてはいかがでしょうか。
最後までお読みくださり、ありがとうございました。



