・今回は、機械設計において重要な動力計算について書いてみたいと思います。
ここでの動力計算とは、動力源である電動機:モータに必要な電気容量を算出する
ことをいいます。
この記事は、設計初心者から中級者の方に向けた内容です。
基礎的なことから詳しく、そしてどんなパターンにも使えるような内容にしています。
動力計算で悩んでおられる方は、この記事を参考にしてもらえればと思います。
計算機能もありますので、よかったら活用してください。
計算に必要な引用元資料を多くリンクしていますので、根拠が必要な場合に
確認していただければと思います。
それではどうぞ。

・最初に、何をどのように、どこからどこへ動かすのかを
明確にしましょう。
代表的な機構を以下に示していきます。
昇降機構
荷物をまっすぐ上に持ち上げていく場合です。
エレベータやクレーンなどが該当します。
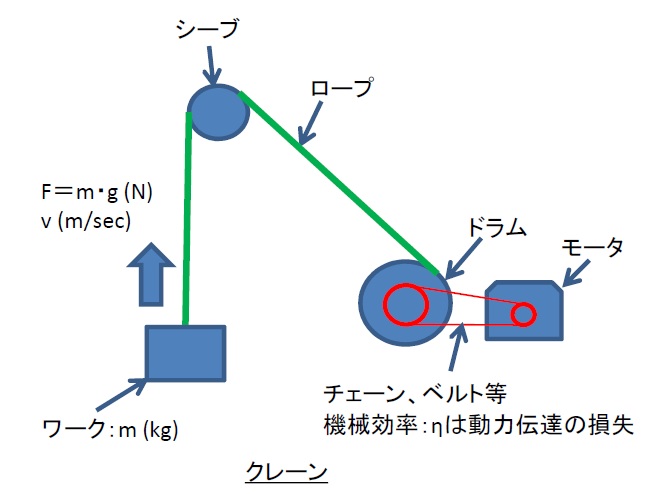
計算式は以下になります。
動力:\(P=\large{\frac{mgv}{1000η}}\normalsize{(kW)}\)
gは、重力加速度:9.80665\((m/sec^2)\)
なので、分母の1000をgで割って整理すると
\(\large{\frac{1000}{g}}\normalsize{=}\large{\frac{1000}{9.80665}}\normalsize{=102}\)より
P=mv/(102η) (kW)
となります。
つまり、質量、速度と機械効率の3つがわかれば、
動力は計算することができるのです。
簡単ですよね。
この式で基本的に全て通用します。
η は、イータと読みます。
工学では、効率を表す記号として使われます。
そして、あと重要なのは作用している力:\(F=mg\) です。
床の上を滑らせたり、転がしたりすることで力が変わります。
よって、機構によって違ってくる式になるので他の機構で説明します。
ここで、改めて今回の式の計算機能を以下に示します。
ただし、機械効率はそんなに厳密な精度を求める必要はありません。
理由は、モータ容量には定格値があって、
計算値に対して最後に安全率:1.5~2.0を
かけて、その値以上の容量を選定するからです。
以降に機械効率の参考情報を記載していますが、温度等に
よって変わってきますので、様々な条件を考慮して設定してください。
平行軸:平歯車などの場合、\(η=0.98~0.995\)
交差軸:かさ歯車などの場合、\(η=0.98~0.99\)
食い違い軸:ウォームホイールなどの場合、\(η=0.3~0.9\)
引用元資料はこちらを参照ください。
引用元の資料では、機械効率のことを伝達効率と称して記載しています。
公的機関の資料はこちらですが、試験等によって求めよとされています。
大洋製器工業さんの資料では、0.96と仮定して計算例を示しています。
この値は大きく外れていないと思います。
よって、0.90~0.96程度だと推察します。
大洋製器工業さんの資料は、サイトから削除されてしまいました。
こちらを参照してください。
で掲載しているので、確認してみてください。
ただし、効率ではなくて出力トルクを示している
カタログが多いです。
1例として、椿本チエインさんのHPのこちらを参照ください。
よって、次はトルクから動力を計算する式をご紹介します。
トルクと動力の計算式
まず、最初に登場した簡単な動力計算の式から変形していきます。
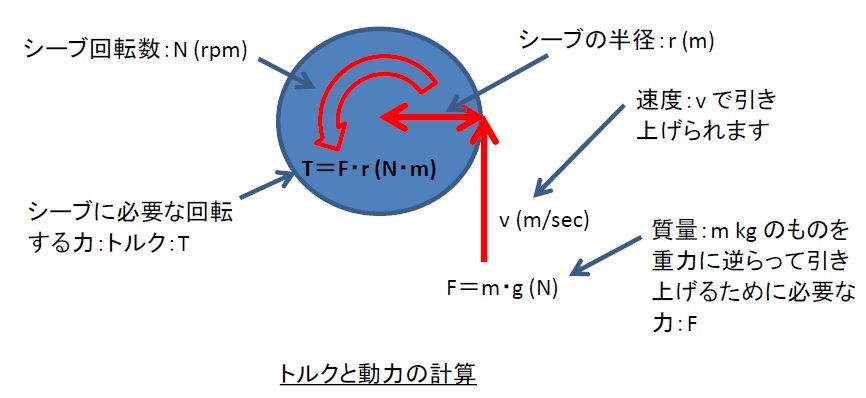
トルク:\(T (N・m)\) は
\(T=Fr=mgr\)より
\(mg=\large{\frac{T}{r}}\) を以下の式に代入すると
\(P=\large{\frac{mgv}{1000η}}\)
\(P=\large{\frac{Tv}{1000rη}}\) となります。
速度:\(v (m/sec)\)は、回転数:\(N (rpm)\)を用いて
以下のように表すことができます。
\(v=\large{\frac{2πrN}{60}}\)
よって、
\(P=\large{\frac{T}{r}}\normalsize{\times}\large{\frac{2πrN}{60\times1000η}}\)
=2・π・T・N/(60000・η )
ここで、分母の60000を2πで割ると
60000/(2・π)≒9549より
P=T・N/(9549・η ) (kW)
となります。
計算機能を以下に示します。
コンベア機構
荷物:ワークを水平または傾斜したコンベアで搬送する場合です。
ベルトコンベアやローラコンベアが該当します。

計算式は以下です。
動力:P=m・g・μ・v/(1000・η ) (kW) より
P=m・μ・v/(102・η ) (kW)
さきほどの引き上げ動力計算の式:P=m・v/(102・η )
に、μ が追加されただけなのがおわかりいただけますよね。
摩擦係数:μ については後でご説明します。
計算機能を以下に示します。

計算式は以下です。
動力:Pは
P=m(sinθ+μ・cosθ)v/(102・η ) (kW)
計算機能を以下に示します。
ベルトをガイドの上で滑らせると、進行方向とは
逆方向に抵抗する力が発生します。
抵抗する力は、搬送面に対して垂直方向の力に摩擦係数を
かけた値になります。
つまり、水平であれば、F=m・g・μ
角度:θの傾斜面であれば、F=m・g・μ・cosθ
となります。
摩擦係数のデータはミスミさんのこちらを参照ください。
いろんな材質どうしの摩擦係数が載っています。
機械工学便覧にも同じようなデータが記載されています。
ベルトメーカーのデータも一例としてこちらを参照ください。
ガイドではなく、ローラーの上を転がす場合は、
ローラーに装備されているブッシュの摩擦係数や
ベアリングの転がり摩擦係数になります。
こちらを参照ください。
ボールねじ機構
これもコンベアと似ています。
ベルトコンベアやローラコンベアと違って、
連続搬送はできません。
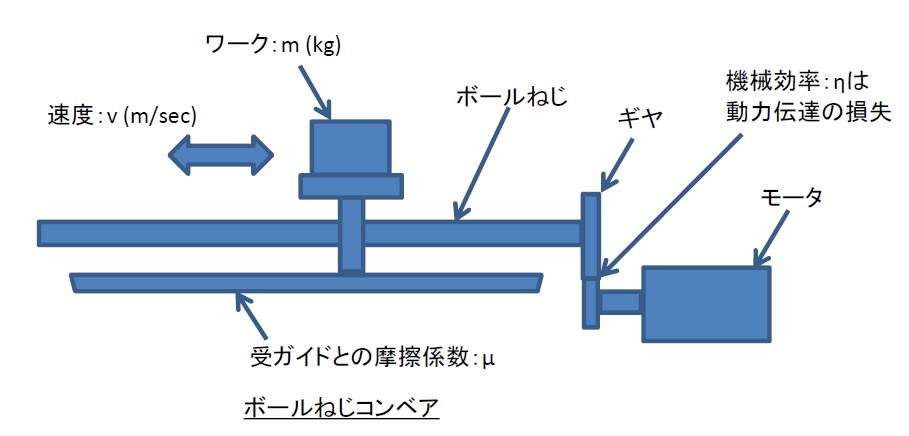
ボールねじ機構は、停止位置精度が高く応用がきくので
いろんな使い方ができますが、ベルトコンベアや
ローラコンベアと比較すると高価になります。
計算式は以下になります。
動力:Pは
P=m・μ・v/(102・η ) (kW)
この式は、コンベアの式と同じです。
ボールねじの機械効率:η は、0.9~0.95ぐらいです。
ざっと動力検討する時は、だいたいこのくらいの値で
計算すればじゅうぶんです。
リード角によって異なりますので、選定した際に
妥当かどうかを確認しましょう。
ほとんどのボールねじのリード角は5度以上です。
詳細は、こちらを参照ください。
計算機能を以下に示します。
ドア開閉機構
引きドアだったり、開きドアがあります。

計算式は以下になります。
動力:Pは、
P=m・μ・v/(102・η ) (kW)
水平の場合のコンベア動力計算と同じです。
計算機能を以下に示します。

計算式は以下のトルクと動力の式を使います。
動力:P=T・N/(9549・η ) (kW)
・回転数:N (rpm)は、角速度:ω (rad/sec)から求めることができます。
N=ω/(2π)・60 (rpm)
・トルク:T (N・m)は、この場合ドアの支点に作用している力:Fに
回転軸径:d (m)の半径:d/2と摩擦係数:μをかけたものになります。
よって、
F=m・g・r/H より
トルクはFにd/2とμをかけるので
T=m・g・r・μ・d/(2H) (N)
となります。
これを最初のトルクと動力の式に代入すると、
動力:P は
P=m・g・r・μ・d・N/(9549・2H・η ) (kW)
となります。
計算機能を以下に示します。
まとめ
・いろんな機構の動力計算式をご紹介しましたが、
基本式は、
P=m・v/(102・η )
であることがご理解いただけたと思います。
クレーン、コンベア、ボールねじ、ドアなど、
基本式に少し変形を加える場合がありますが、
ほとんどの機構に適用できます。
開きドアの式が少しややこしかったですね。
・あと考える必要があるのが、停止した状態から所定の
速度にまで加速するのに必要な加速力です。
通常は所定の速度を出すために必要な動力と、
加速に必要な動力を足し合わせてモータ容量を決定します。
加速力が動力に大きく影響するのは、早く加速させたり、
ワークの質量が大きい場合です。
よって、次回は加速力についてご紹介したいと思います。
最後までお読みくださり、ありがとうございました



